本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准如下:每车每次租若不超过两小时,则免费;超过两小时的部分为每小时2元(不足1小时的部分按1小时计算). 甲、乙独立来该租车点 租车骑游,各租一车一次.设甲、乙不超过两小
租车骑游,各租一车一次.设甲、乙不超过两小 时还车的概率分别为
时还车的概率分别为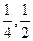 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为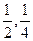 ;两人租车时间都不会超过四小
;两人租车时间都不会超过四小 时.
时.
(Ⅰ)求出甲、乙所付 租车费用相同的概率;
租车费用相同的概率;
(Ⅱ)设甲、乙两人所付的租车费用之和为随机变量
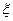 ,求
,求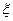 的分布列与数学期望
的分布列与数学期望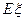 .
.
推荐套卷
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准如下:每车每次租若不超过两小时,则免费;超过两小时的部分为每小时2元(不足1小时的部分按1小时计算). 甲、乙独立来该租车点 租车骑游,各租一车一次.设甲、乙不超过两小
租车骑游,各租一车一次.设甲、乙不超过两小 时还车的概率分别为
时还车的概率分别为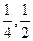 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为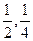 ;两人租车时间都不会超过四小
;两人租车时间都不会超过四小 时.
时.
(Ⅰ)求出甲、乙所付 租车费用相同的概率;
租车费用相同的概率;
(Ⅱ)设甲、乙两人所付的租车费用之和为随机变量
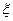 ,求
,求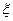 的分布列与数学期望
的分布列与数学期望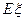 .
.