某医疗研究所为了检验某种血清预防感冒的作用,把 名使用血清的人与另外
名使用血清的人与另外 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设 :“这种血清不能起到预防感
:“这种血清不能起到预防感 冒的作用”,利用
冒的作用”,利用 列联表计算得
列联表计算得 ,经查对临界
,经查对临界 值表知
值表知 .对此,四名同学做出了以下的判断:
.对此,四名同学做出了以下的判断: :有
:有 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用” :若某人未使用该血清,那么他在一年中有
:若某人未使用该血清,那么他在一年中有 的可能性得感冒
的可能性得感冒 :这种血清预防感冒的有效率为
:这种血清预防感冒的有效率为
 :这种血清预
:这种血清预 防感冒的有效率为
防感冒的有效率为
则下列结论中,正确结论的序号是
①  ; ②
; ② ; ③
; ③ ; ④
; ④
相关知识点
推荐套卷
 的展开式中的常数项是.
的展开式中的常数项是. 将
将 用“
用“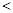 ”号连接起来为.
”号连接起来为.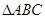 中,角
中,角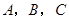 所对的边分别为
所对的边分别为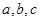 ,角
,角 为锐角,且
为锐角,且 ,则
,则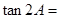 .
.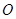 的位移
的位移 和时间
和时间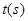 的函数关系为
的函数关系为 ,那么单摆来回摆动一次所需的时间为 .
,那么单摆来回摆动一次所需的时间为 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号