等比数列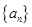 中,
中,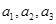 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且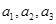 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| |
第一列 |
第二列 |
第三列 |
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ) 求数列
求数列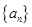 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足: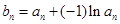 ,求数列
,求数列 的前
的前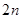 项和
项和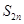 .
.
推荐套卷
等比数列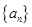 中,
中,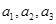 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且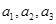 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| |
第一列 |
第二列 |
第三列 |
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ) 求数列
求数列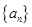 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足: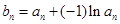 ,求数列
,求数列 的前
的前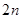 项和
项和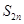 .
.