从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,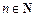 )共有
)共有 种取法.在这
种取法.在这 种取法中,可以分成两类:一类是取出的m个球全部为白球,共
种取法中,可以分成两类:一类是取出的m个球全部为白球,共
有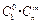 种取法;另一类是取出的m个球有
种取法;另一类是取出的m个球有 个白球和1个黑球,共有
个白球和1个黑球,共有 种取法.显然
种取法.显然 立,即有等式:
立,即有等式: .试根据上述思想,类比化简下列式子:
.试根据上述思想,类比化简下列式子: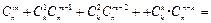
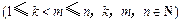 .
.
推荐套卷
从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,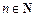 )共有
)共有 种取法.在这
种取法.在这 种取法中,可以分成两类:一类是取出的m个球全部为白球,共
种取法中,可以分成两类:一类是取出的m个球全部为白球,共
有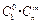 种取法;另一类是取出的m个球有
种取法;另一类是取出的m个球有 个白球和1个黑球,共有
个白球和1个黑球,共有 种取法.显然
种取法.显然 立,即有等式:
立,即有等式: .试根据上述思想,类比化简下列式子:
.试根据上述思想,类比化简下列式子: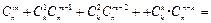
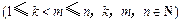 .
.