某射手射击1次，击中目标的概率是0.9，他连续射击4次，且各次射击是否击中目标相互之间没有影响，有下列结论：
①他第3次击中目标的概率是0.9；②他恰好击中目标3次的概率是0.93×0.1；
③他至少击中目标1次的概率是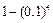
．
其中正确结论的序号是 （写出所有正确结论的序号）．
中，
，则角A的值为__________.
，BC＝2，C＝60°，则边AB的长度等于________．
到平面
的距离是.
的模为____________推荐套卷
某射手射击1次，击中目标的概率是0.9，他连续射击4次，且各次射击是否击中目标相互之间没有影响，有下列结论：
①他第3次击中目标的概率是0.9；②他恰好击中目标3次的概率是0.93×0.1；
③他至少击中目标1次的概率是．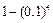
其中正确结论的序号是 （写出所有正确结论的序号）．
粤公网安备 44130202000953号