给出下列四个命题：
①过平面外一点，作与该平面成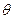
角的直线一定有无穷多条。
②一条直线与两个相交平面都平行，则它必与这两个平面的交线平行；
③对确定的两条异面直线，过空间任意一点有且只有一个平面与这两条异面直线都平行；
④对两条异面的直线，都存在无穷多个平面与这两条直线所成的角相等；
其中正确的命题序号为:
推荐套卷
给出下列四个命题：
①过平面外一点，作与该平面成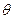角的直线一定有无穷多条。
②一条直线与两个相交平面都平行，则它必与这两个平面的交线平行；
③对确定的两条异面直线，过空间任意一点有且只有一个平面与这两条异面直线都平行；
④对两条异面的直线，都存在无穷多个平面与这两条直线所成的角相等；
其中正确的命题序号为:
粤公网安备 44130202000953号