(本小题满分12分)如题(21)图,已知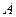 、
、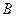 为椭圆
为椭圆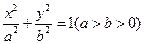 和双曲线
和双曲线 的公共顶点,
的公共顶点, 、
、 分别为双曲线和椭圆上不同于
分别为双曲线和椭圆上不同于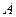 、
、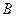 的动点,且
的动点,且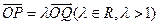 .设
.设 、
、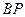 、
、 、
、 的斜率分别为
的斜率分别为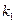 、
、 、
、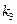 、
、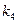 .
.
(I)求证: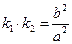 ;
;
(II)求 的值;
的值;
(III)设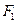 、
、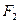 分别为双曲线和椭圆的右焦点,若
分别为双曲线和椭圆的右焦点,若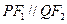 ,求
,求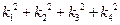 的值.
的值.
推荐套卷
(本小题满分12分)如题(21)图,已知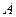 、
、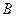 为椭圆
为椭圆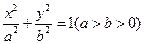 和双曲线
和双曲线 的公共顶点,
的公共顶点, 、
、 分别为双曲线和椭圆上不同于
分别为双曲线和椭圆上不同于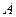 、
、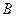 的动点,且
的动点,且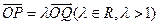 .设
.设 、
、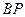 、
、 、
、 的斜率分别为
的斜率分别为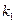 、
、 、
、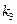 、
、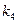 .
.
(I)求证: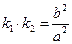 ;
;
(II)求 的值;
的值;
(III)设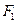 、
、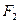 分别为双曲线和椭圆的右焦点,若
分别为双曲线和椭圆的右焦点,若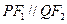 ,求
,求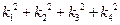 的值.
的值.