杨辉是中国南宋末年的一位杰出的数学家、数学教育家,他的数学研究与教育工作的重点是在计算技术方面,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关. 图2是一个7阶的杨辉三角.
 |
给出下列五个命题:
①记第 行中从左到右的第
行中从左到右的第 个数为
个数为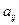 ,则数列
,则数列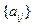 的通项公式为
的通项公式为 ;
;
②第k行各数的和是 ;
;
③n阶杨辉三角中共有 个数;
个数;
④n阶杨辉三角的所有数的和是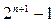 .
.
其中正确命题的序号为___________________.
推荐套卷
杨辉是中国南宋末年的一位杰出的数学家、数学教育家,他的数学研究与教育工作的重点是在计算技术方面,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关. 图2是一个7阶的杨辉三角.
 |
给出下列五个命题:
①记第 行中从左到右的第
行中从左到右的第 个数为
个数为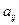 ,则数列
,则数列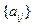 的通项公式为
的通项公式为 ;
;
②第k行各数的和是 ;
;
③n阶杨辉三角中共有 个数;
个数;
④n阶杨辉三角的所有数的和是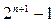 .
.
其中正确命题的序号为___________________.