有10名同学高一(x)和高二(y)的数学成绩如下:
| 高一成绩x |
74 |
71 |
72 |
68 |
76 |
73 |
67 |
70 |
65 |
74 |
| 高二成绩y |
76 |
75 |
71 |
70 |
76 |
79 |
65 |
77 |
62 |
72 |
(1)画出散点图;
(2)求y对x的回归方程.
相关知识点
推荐套卷
 ),若其展开式中,关于x的一次项系数为11,试问:m、n取何值时,f(x)的展开式中含x2项的系数取最小值,并求出这个最小值.
),若其展开式中,关于x的一次项系数为11,试问:m、n取何值时,f(x)的展开式中含x2项的系数取最小值,并求出这个最小值.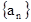 ,使
,使 对任意
对任意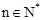 都成立?若存在,求出数列
都成立?若存在,求出数列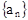 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.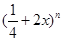 的展开式中前三项的二项式系数的和等于37,求展式中二项式系数最大的项的系数.
的展开式中前三项的二项式系数的和等于37,求展式中二项式系数最大的项的系数.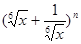 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列. 粤公网安备 44130202000953号
粤公网安备 44130202000953号