下列命题中:
①设 {直线},
{直线}, {圆},则集合
{圆},则集合 的元素个数为:0或1或2;
的元素个数为:0或1或2;
②过抛物线 :
: 的焦点
的焦点 作直线
作直线 交抛物线
交抛物线 于
于 两点,则
两点,则 ;
;
③已知二面角 的平面角的大小是
的平面角的大小是 ,
, ,
, ,
, 是直线
是直线 上的
上的 任意一点,过点
任意一点,过点 与
与 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 ,且
,且 ,则
,则 的最小值为:
的最小值为: ;
;
④已知 是平面,
是平面, 是直线,若
是直线,若 ,则
,则 ;
;
⑤已知点M是抛物线 上的一点,F为抛物线的焦点,点A在圆
上的一点,F为抛物线的焦点,点A在圆 上,
上,
则 的最小值为4;
的最小值为4;
以上命题正确的为 (把所有正确的命题序号写在横线上)。
相关知识点
推荐套卷
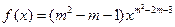 是幂函数,且在
是幂函数,且在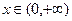 上是减函数,则实数
上是减函数,则实数 .
. 元,每期利率为
元,每期利率为 ,存期为
,存期为 ,则本利和
,则本利和 随存期
随存期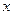 变化的函数解析式为.
变化的函数解析式为.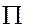 ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作 ,
, ,其中
,其中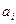 为数列
为数列 中的第
中的第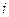 项.
项.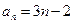 ,则
,则 = ; ②若
= ; ②若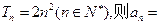
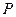
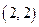 在曲线
在曲线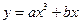 上,如果该曲线在点
上,如果该曲线在点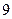 ,那么
,那么 ,此时函数
,此时函数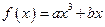 ,
,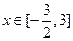 的值域为
的值域为 时,
时, ,且
,且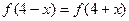 恒成立,则当
恒成立,则当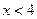 时,
时, =
= 粤公网安备 44130202000953号
粤公网安备 44130202000953号