经济学中的“蛛网理论”(如下图),假定某种商品的“需求—价格”函数的图像为直线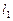 ,“供给—价格”函数的图像为直线
,“供给—价格”函数的图像为直线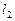 ,它们的斜率分别为
,它们的斜率分别为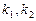 ,
,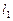 与
与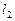 的交点
的交点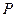 为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点
为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点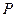 ,与直线
,与直线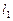 、
、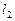 的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点
的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点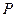 的条件为 ( )
的条件为 ( )
A.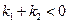 |
B.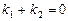 |
C.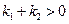 |
D.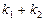 可取任意实数 可取任意实数 |
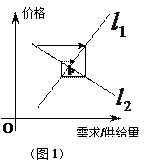 |
|||||
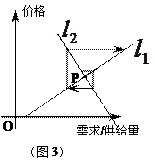 |
|||||
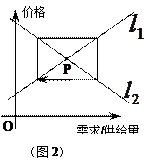 |
|||||
推荐套卷
 ,猜想
,猜想 的一个表达式为( ▲ )
的一个表达式为( ▲ )



 ,
, ;②
;② ,
, ;
; ,
, ;④
;④ ,
,
 为偶函数,则
为偶函数,则 ( ).
( ).


 ,则(▲ )
,则(▲ )



 如果
如果 (其中
(其中 ),则
),则 (▲)
(▲)



 粤公网安备 44130202000953号
粤公网安备 44130202000953号