已知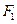
、
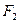分别是椭圆C:
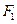的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过的弦AB两端点A、B与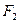所成
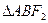的周长是
.
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点
，
是椭圆C上不同的两点，线段
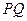的中点为
,
求直线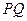的方程
中，角A,B,C,的对边分别为
，且
的值；
，求
是各项均为正数的等比数列，且
，
求数列
的前
项和
.
的不等式
.
，x∈R(其中A＞0，ω＞0,
)的周期为π，且图象上一个最低点为M
.
时，求f(x)的最大值．
求
的值域.推荐套卷
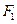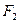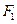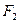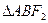已知、分别是椭圆C:的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过的弦AB两端点A、B与所成的周长是.
（Ⅰ）求椭圆C的标准方程；
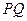（Ⅱ）已知点，是椭圆C上不同的两点，线段的中点为,
求直线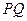的方程
粤公网安备 44130202000953号