设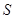
是至少含有两个元素的集合，在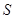上定义了一个二元运算“*”（即
对任意的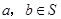
，对于有序元素对（
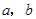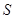），在中有唯一确定的元
素
与之对应）．若对任意的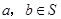，有
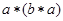
，则对任意
的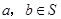，下列等式中不恒成立的是（ ）
A． |
B． |
C． |
D． |
的前n项和为
，且
，
，则
（）
，
，则（）
推荐套卷
设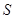是至少含有两个元素的集合，在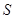上定义了一个二元运算“*”（即
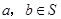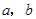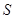对任意的，对于有序元素对（），在中有唯一确定的元
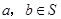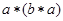
素与之对应）．若对任意的，有，则对任意
的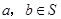，下列等式中不恒成立的是（ ）
| A． |
B． |
| C． |
D． |
粤公网安备 44130202000953号