(文)(本小题8分)
如图,在四棱锥 中,
中, 平面
平面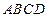 ,
,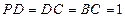 ,
,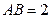 ,
, ,
,
(1)求证: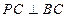 ;
;
(2)求点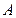 到平面
到平面 的距离
的距离
证明:(1) 平面
平面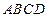 ,
, 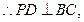 又
又
 平面
平面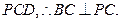
(2)设点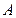 到平面
到平面 的距离为
的距离为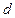 ,
, ,
, ,
,
求得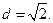 即点
即点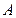 到平面
到平面 的距离为
的距离为
(其它方法可参照上述评分标准给分)
推荐套卷
(文)(本小题8分)
如图,在四棱锥 中,
中, 平面
平面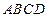 ,
,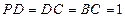 ,
,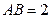 ,
, ,
,
(1)求证: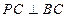 ;
;
(2)求点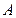 到平面
到平面 的距离
的距离
证明:(1) 平面
平面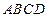 ,
, 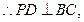 又
又
 平面
平面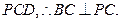
(2)设点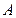 到平面
到平面 的距离为
的距离为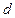 ,
, ,
, ,
,
求得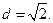 即点
即点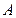 到平面
到平面 的距离为
的距离为
(其它方法可参照上述评分标准给分)