要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表所示:
| 类 型 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
1 |
2 |
1 |
| 第二种钢板 |
1 |
1 |
3 |
每张钢板的面积,第一种为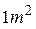 ,第二种为
,第二种为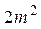 ,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
推荐套卷
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表所示:
| 类 型 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
1 |
2 |
1 |
| 第二种钢板 |
1 |
1 |
3 |
每张钢板的面积,第一种为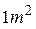 ,第二种为
,第二种为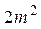 ,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?