用反证法证明命题:若系数都为整数的一元二次方程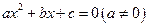 有有理根,那么
有有理根,那么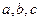 中至少有一个是偶数。下列假设中正确的是( )
中至少有一个是偶数。下列假设中正确的是( )
A.假设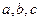 都是偶数 都是偶数 |
B.假设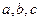 都不是偶数 都不是偶数 |
C.假设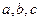 中至多有一个偶 中至多有一个偶 数 数 |
D.假设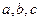 中至多有两个偶数 中至多有两个偶数 |
推荐套卷
用反证法证明命题:若系数都为整数的一元二次方程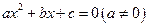 有有理根,那么
有有理根,那么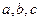 中至少有一个是偶数。下列假设中正确的是( )
中至少有一个是偶数。下列假设中正确的是( )
A.假设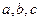 都是偶数 都是偶数 |
B.假设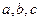 都不是偶数 都不是偶数 |
C.假设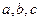 中至多有一个偶 中至多有一个偶 数 数 |
D.假设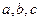 中至多有两个偶数 中至多有两个偶数 |