（本小题满分12分）
如图，
平面ABC，EB//DC，AC=BC=EB=2DC=2，
，P、Q分别为DE、AB的中点。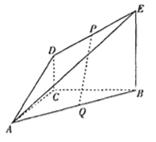
（Ⅰ）求证：PQ//平面ACD；
（Ⅱ）求几何体B—ADE的体积；
（Ⅲ）求平面ADE与平面ABC所成锐二面角的正切值。
相关试题
．（1）求函数
的单调区间；
的方程
有实数解,求实数
的取值范围；
时,求证：
．
中，
，四边形
是边长为
的正方形，若
分别是线段
的中点．
∥底面
；
为线段
的中点，求三角形
的面积．
．（1）当
时，求
的值域；（2）若△ABC的内角A，B，C的对边分别为
，且满足
，
，求
的值．
中，
，
（
），
是数列
；（2）设数列
满足
（
项和
．
是公差不为0的等差数列
的前n项和，且
成等比数列，
．
，
是数列
的前n项和，求使得
对所有
都成立的最小正整数
．推荐套卷
（本小题满分12分）
如图，平面ABC，EB//DC，AC=BC=EB=2DC=2，，P、Q分别为DE、AB的中点。
（Ⅰ）求证：PQ//平面ACD；
（Ⅱ）求几何体B—ADE的体积；
（Ⅲ）求平面ADE与平面ABC所成锐二面角的正切值。
粤公网安备 44130202000953号