(本小题满分12分)
已知定义在R上的函数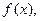 满足条件:
满足条件: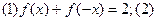 对非零实数
对非零实数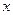 ,
,
都有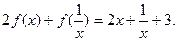
(1) 求函数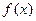 的解析式;
的解析式;
(2) 设函数 直线
直线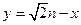 分别与函数
分别与函数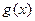 的反函数
的反函数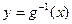 交于A,B两点(其中
交于A,B两点(其中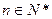 ),设
),设 为数列
为数列 的前
的前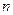 项和.求证:当
项和.求证:当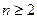 时,总有
时,总有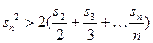 成立.
成立.
推荐套卷
(本小题满分12分)
已知定义在R上的函数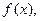 满足条件:
满足条件: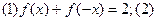 对非零实数
对非零实数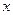 ,
,
都有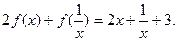
(1) 求函数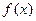 的解析式;
的解析式;
(2) 设函数 直线
直线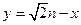 分别与函数
分别与函数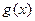 的反函数
的反函数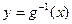 交于A,B两点(其中
交于A,B两点(其中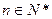 ),设
),设 为数列
为数列 的前
的前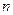 项和.求证:当
项和.求证:当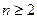 时,总有
时,总有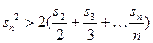 成立.
成立.