(本小题满分12分)
如图5,平面ABDE⊥平面ABC,AC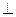 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD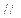 AE,BD
AE,BD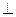 BA,AE=2BD=4,O、M分别为CE、AB的中点.
BA,AE=2BD=4,O、M分别为CE、AB的中点.
(Ⅰ) 证明:OD//平面ABC;
(Ⅱ)能否在EM上找一点N,使得ON⊥平面ABDE?
若能,请指出点N的位置,并加以证明;
若不能,请说明理由.
推荐套卷
(本小题满分12分)
如图5,平面ABDE⊥平面ABC,AC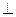 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD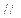 AE,BD
AE,BD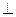 BA,AE=2BD=4,O、M分别为CE、AB的中点.
BA,AE=2BD=4,O、M分别为CE、AB的中点.
(Ⅰ) 证明:OD//平面ABC;
(Ⅱ)能否在EM上找一点N,使得ON⊥平面ABDE?
若能,请指出点N的位置,并加以证明;
若不能,请说明理由.