数列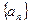 为等,
为等,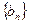 为等比,且
为等比,且 ,
,
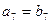 ,关于
,关于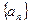 与
与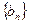 有下列命题:
有下列命题:
①有无数项相同但不是所有项相同②所有项相同③只有两项相同,④有且只有13项相同,
则上述命题中有可能成立的是( )
)
| A.①②③④ | B.①②③ | C.①③④ | D.①②④ |
推荐套卷
数列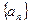 为等,
为等,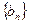 为等比,且
为等比,且 ,
,
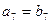 ,关于
,关于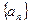 与
与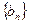 有下列命题:
有下列命题:
①有无数项相同但不是所有项相同②所有项相同③只有两项相同,④有且只有13项相同,
则上述命题中有可能成立的是( )
)
| A.①②③④ | B.①②③ | C.①③④ | D.①②④ |