．在1，2，3，4，5中任取两个不同的数作为坐标构成的平面向量的集合为M。对M中的每一个向量，作与其大小相等且数量积为零的向量，构成向量集合V。分别在向量集合M、V中各任取一个向量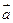
与向量
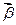，其满足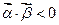
的概率是 （ ）
A． |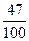
B． |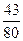
C． |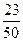
D． |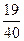
，若
,则实数
的取值范围是（）
，则“
”是“
恒成立”的（）
，则
（）
，集合
，则
=（）
，则
．推荐套卷
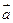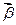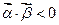．在1，2，3，4，5中任取两个不同的数作为坐标构成的平面向量的集合为M。对M中的每一个向量，作与其大小相等且数量积为零的向量，构成向量集合V。分别在向量集合M、V中各任取一个向量与向量，其满足的概率是 （ ）
| A． |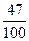
B． |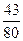
C． |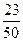
D． |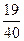
粤公网安备 44130202000953号