((本小题满分12分)
已知椭圆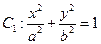 的左、右两个焦点为
的左、右两个焦点为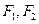 ,离心率为
,离心率为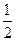 ,又抛物线
,又抛物线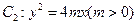 与椭圆
与椭圆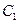 有公共焦点
有公共焦点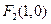 .
.
(1)求椭圆和抛物线的方程;
(2)设直线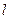 经过椭圆的左焦点
经过椭圆的左焦点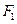 且与抛物线交于不同两点P、Q且满足
且与抛物线交于不同两点P、Q且满足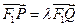 ,求实数
,求实数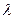 的取值范围.
的取值范围.
推荐套卷
((本小题满分12分)
已知椭圆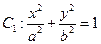 的左、右两个焦点为
的左、右两个焦点为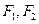 ,离心率为
,离心率为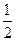 ,又抛物线
,又抛物线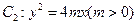 与椭圆
与椭圆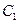 有公共焦点
有公共焦点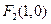 .
.
(1)求椭圆和抛物线的方程;
(2)设直线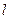 经过椭圆的左焦点
经过椭圆的左焦点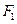 且与抛物线交于不同两点P、Q且满足
且与抛物线交于不同两点P、Q且满足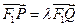 ,求实数
,求实数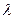 的取值范围.
的取值范围.