(本小题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组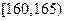 ,第2组
,第2组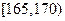 ,第3组
,第3组 ,第4组
,第4组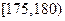 ,第5组
,第5组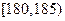 ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。
(1)求第3 、4、5组的频率;
、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
推荐套卷
 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
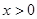 ,求函数
,求函数 的最小值,并求此时x的值.
的最小值,并求此时x的值. ,求函数
,求函数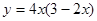 的最大值.
的最大值. 是一个等差数列,且
是一个等差数列,且 ,
, .
. ;(2)求
;(2)求 的最大值.
的最大值.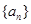 的前
的前 项和为
项和为 且
且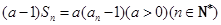 .
.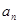 ;
;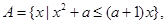 问是否存在实数
问是否存在实数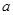 ,使得对于任意的
,使得对于任意的 都有
都有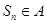 ? 若存在,求出
? 若存在,求出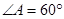 ,P、Q分别是
,P、Q分别是 两边上的动点.
两边上的动点.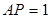 ,
,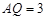 时,求PQ的长;(2)AP、AQ长度之和为定值4,求线段PQ最小值.
时,求PQ的长;(2)AP、AQ长度之和为定值4,求线段PQ最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号