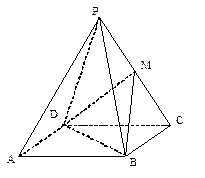已知四边形ABCD是正方形，P是平面ABCD外一点，且PA=PB=PC=PD=AB=2，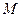
是棱
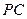的中点．建立适当的空间直角坐标系，利用空间向量方法解答以下问题：
(1)求证：
；
(2) 求证：
；
(3)求直线
与直线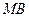
所成角的余弦值．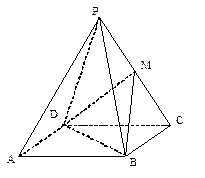
满足约束条件
，则
的最大值为．
(2)＝．
且
，则
的最小值为___ _____．
与
的夹角为
，则称向量“推荐套卷
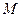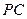已知四边形ABCD是正方形，P是平面ABCD外一点，且PA=PB=PC=PD=AB=2，是棱的中点．建立适当的空间直角坐标系，利用空间向量方法解答以下问题：
(1)求证：；
(2) 求证：；
(3)求直线与直线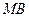所成角的余弦值．
粤公网安备 44130202000953号