命题“在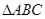
中，若
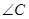是直角，则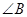
一定是锐角．”的证明过程如下：
假设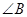不是锐角，则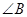是直角或钝角，即
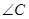，而是直角，
所以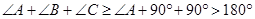
，
这与三角形的内角和等于
矛盾，所以上述假设不成立，
即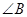一定是锐角．本题采用的证明方法是
| A．综合法 | B．分析法 | C．反证法 | D．数学归纳法 |
相关试题
中，若
，则此数列的前
项和
是（）
是公比为
的等比数列，若
，则
（）
，则下列不等式正确的是（）
＜m＜
＜m＜
，若
，则实数a的取值范围是( )
推荐套卷
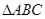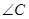命题“在中，若是直角，则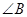一定是锐角．”的证明过程如下：
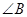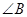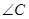假设不是锐角，则是直角或钝角，即，而是直角，
所以，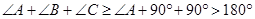
这与三角形的内角和等于矛盾，所以上述假设不成立，
即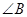一定是锐角．本题采用的证明方法是
| A．综合法 | B．分析法 | C．反证法 | D．数学归纳法 |
粤公网安备 44130202000953号