给出定义：若函数
在
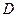上可导，即
存在，且导函数在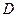上也可导，则称在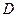上存在二阶导函数，记
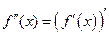，若
在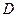上恒成立，则称在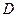上为凸函数。以下四个函数在
上不是凸函数的是（ ）
A． |
B． |
C． |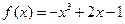
D． |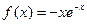
的值应是
都是实数，i是虚数单位，则
=""
,则实数a的取值范围是
均为锐角，且
，则
的大小关系为（）
－x）sinx在［0，π］
推荐套卷
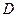给出定义：若函数在上可导，即存在，且导函数在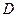上也可导，则称在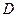上存在二阶导函数，记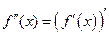，若在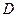上恒成立，则称在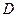上为凸函数。以下四个函数在上不是凸函数的是（ ）
| A． |
B． |
C． |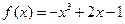
D． |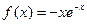
粤公网安备 44130202000953号