（本小题满分13分）
已知m,n表示先后抛掷一个骰子所得到正面向上的点数，方程C：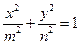
（1）求共可以组成多少个不同的方程C；
（2）求能组成落在区域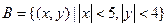
且焦点在X轴的椭圆的概率；
（3）在已知方程C为落在区域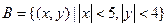且焦点在X轴的椭圆的情况下，求离心率为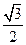
的概率
相关试题
中，a1=2,an+1=an+cn(c是常数，n=1,2,3……)且a1,a2,a3成公比不为1的等比数列
bc，求：
，过点
作抛物线的两条切线
，切点分别为
.
过定点
；
（
为坐标原点）面积的最小值.
的底面为矩形，
且
平面
分别为
的中点.
；
的大小值.
推荐套卷
（本小题满分13分）
已知m,n表示先后抛掷一个骰子所得到正面向上的点数，方程C：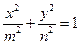
（1）求共可以组成多少个不同的方程C；
（2）求能组成落在区域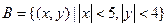且焦点在X轴的椭圆的概率；
（3）在已知方程C为落在区域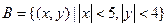且焦点在X轴的椭圆的情况下，求离心率为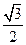的概率
粤公网安备 44130202000953号