一组抛物线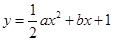
，其中
为2,4,6,8中任取的一个数，
为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线
交点处的切线相互平行的概率是（ ）
A． |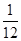
B． |
C． |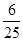
D． |
相关试题
对应的复数是5-4i，向量
对应的复数是-5+4i，则
对应的复数是( )
的实部与虚部之和为（）
，都有
，若
在区间
上是凸函数，那么在
中，
的最大值为（）
的值为（）
相关知识点
推荐套卷
一组抛物线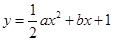，其中为2,4,6,8中任取的一个数，为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线交点处的切线相互平行的概率是（ ）
| A． |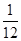
B． |
C． |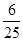
D． |
粤公网安备 44130202000953号