已知双曲线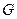 的中心在原点,它的渐近线与圆
的中心在原点,它的渐近线与圆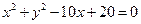 相切. 过点
相切. 过点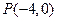 作斜率为
作斜率为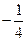 的直线
的直线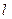 ,使
,使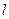 和
和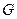 交于
交于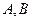 两点,和
两点,和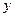 轴交于
轴交于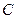 点,且点
点,且点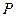 在线段
在线段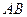 上,满足
上,满足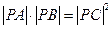
(I)求双曲线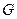 的渐近线方程;
的渐近线方程;
(II)求双曲线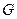 的方程;
的方程;
(Ⅲ)椭圆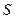 的中心在原点,它的短轴是
的中心在原点,它的短轴是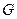 的实轴. 若
的实轴. 若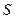 中垂直于
中垂直于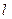 的平行弦的中点的轨迹恰好是
的平行弦的中点的轨迹恰好是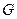 的渐近线截在
的渐近线截在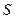 内的部分,求椭圆
内的部分,求椭圆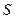 的方程.
的方程.
相关知识点
推荐套卷
已知双曲线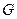 的中心在原点,它的渐近线与圆
的中心在原点,它的渐近线与圆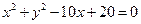 相切. 过点
相切. 过点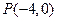 作斜率为
作斜率为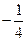 的直线
的直线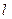 ,使
,使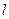 和
和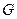 交于
交于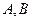 两点,和
两点,和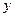 轴交于
轴交于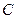 点,且点
点,且点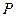 在线段
在线段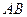 上,满足
上,满足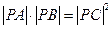
(I)求双曲线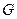 的渐近线方程;
的渐近线方程;
(II)求双曲线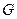 的方程;
的方程;
(Ⅲ)椭圆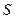 的中心在原点,它的短轴是
的中心在原点,它的短轴是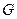 的实轴. 若
的实轴. 若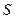 中垂直于
中垂直于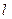 的平行弦的中点的轨迹恰好是
的平行弦的中点的轨迹恰好是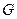 的渐近线截在
的渐近线截在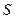 内的部分,求椭圆
内的部分,求椭圆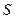 的方程.
的方程.