某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒; …… 第六组,成绩大于等于18秒且小于等于19秒.
下图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒的学生人数占全班总人数的百分比为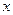 , 成绩大于等于15秒且小于17秒的学生人数为
, 成绩大于等于15秒且小于17秒的学生人数为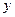 ,则从频率分布直方图中可分析出x和y分别为( )
,则从频率分布直方图中可分析出x和y分别为( )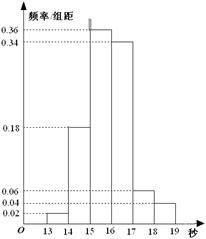
| A.0.9,35 | B.0.9,45 | C.0.1,35 | D.0.1,45 |
推荐套卷
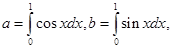 下列关系式成立的是( )
下列关系式成立的是( ) 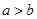 B
B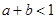 C
C D
D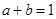
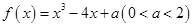 有三个零点
有三个零点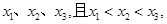 则下列结论正确的是()
则下列结论正确的是()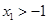

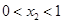
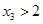
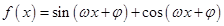
 的最小正周期为
的最小正周期为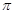 ,且
,且 ,则( )
,则( ) 在
在 单调递减
单调递减 单调递减
单调递减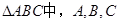 的对边分别为
的对边分别为 ,若
,若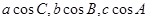 成等差数列则
成等差数列则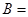 ()
()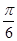



 满足不等式组
满足不等式组  则
则 的最大值是( )
的最大值是( ) 粤公网安备 44130202000953号
粤公网安备 44130202000953号