(满分12分)
已知正方体ABCD—A1B1C1D1,其棱长为2,O是底ABCD对角线的交点。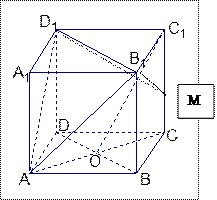
求证:
(1)C1O∥面AB1D1;
(2)A1C⊥面AB1D1。
(3)若M是CC1的中点,求证:平面AB1D1⊥平面MB1D1
推荐套卷
(满分12分)
已知正方体ABCD—A1B1C1D1,其棱长为2,O是底ABCD对角线的交点。
求证:
(1)C1O∥面AB1D1;
(2)A1C⊥面AB1D1。
(3)若M是CC1的中点,求证:平面AB1D1⊥平面MB1D1