古希腊人常用小石子在沙滩上摆成各种性状来研究数，例如：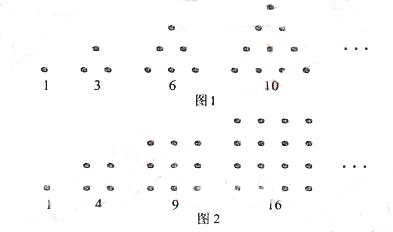 
他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数;类似地，称图2中的1，4，9，16…这样的数成为正方形数。下列数中既是三角形数又是正方形数的是
| A．289 | B．1024 | C．1225 | D．1378 |
相关试题
是该沙漏中沙面下降的高度，则
的函数关系用图象表示应该是（）
的左焦点与抛物线
的焦点的连线平行于该双曲线的一条渐近线，则双曲线的离心率为（）
中，AB=BC=2，
，则
与平面
所成角的余弦值为（）
，则判断框中应填（）
”的否定是“
”
”是“
为偶函数”的充要条件
时，幂函数
上单调递减推荐套卷
古希腊人常用小石子在沙滩上摆成各种性状来研究数，例如：
他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数;类似地，称图2中的1，4，9，16…这样的数成为正方形数。下列数中既是三角形数又是正方形数的是
| A．289 | B．1024 | C．1225 | D．1378 |
粤公网安备 44130202000953号