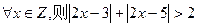给定下列四个命题，其中为真命题的是 （填上所有真命题的序号）
1）命题“若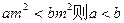
”的逆命题.
2）
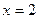是
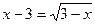的充分不必要条件.
3）已知双曲线
和椭圆
的离心率之积大于1，则以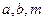
为边长的三角形是钝角三角形.
4)
的图象是折线段ABC，其中A，B，C的坐标分别为
,
．
的值是
，若前n项的和为10，则项数n为_____．
的解集为
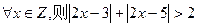
，则m的值为.相关知识点
推荐套卷
给定下列四个命题，其中为真命题的是 （填上所有真命题的序号）
1）命题“若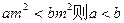”的逆命题.
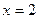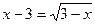2）是的充分不必要条件.
3）已知双曲线和椭圆的离心率之积大于1，则以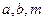为边长的三角形是钝角三角形.
4)
粤公网安备 44130202000953号