给出下列命题:
①若椭圆长轴长与短轴长的和为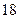 ,焦距为
,焦距为 ,则椭圆的标准方程为
,则椭圆的标准方程为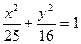 ;
;
②曲线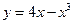 在点
在点 处的切线方程是
处的切线方程是 ;
;
③命题“若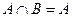 ,则
,则 ”的逆否命题是:“若
”的逆否命题是:“若 ,则
,则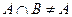 ”;
”;
④高台跳水运动员在 秒时距水面高度
秒时距水面高度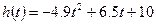 (单位:米),则该运动员的初速度为
(单位:米),则该运动员的初速度为 (米/秒);
(米/秒);
⑤“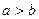 ”是“
”是“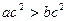 ”的充分条件。
”的充分条件。
正确的命题是 。
推荐套卷
给出下列命题:
①若椭圆长轴长与短轴长的和为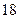 ,焦距为
,焦距为 ,则椭圆的标准方程为
,则椭圆的标准方程为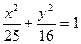 ;
;
②曲线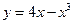 在点
在点 处的切线方程是
处的切线方程是 ;
;
③命题“若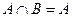 ,则
,则 ”的逆否命题是:“若
”的逆否命题是:“若 ,则
,则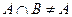 ”;
”;
④高台跳水运动员在 秒时距水面高度
秒时距水面高度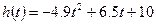 (单位:米),则该运动员的初速度为
(单位:米),则该运动员的初速度为 (米/秒);
(米/秒);
⑤“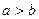 ”是“
”是“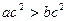 ”的充分条件。
”的充分条件。
正确的命题是 。