如图，直三棱柱
ABC—A1B1C1的底面是等腰直角三角形，∠A1C1B1=90°，A1C1=1，AA1=
，D是线段A1B1的中点．
（1）证明：面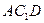
⊥平面A1B1BA；
（2）证明：
；
（3）求棱柱ABC—A1B1C1被平面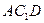分成两部分
的体积比．
推荐套卷
如图，直三棱柱ABC—A1B1C1的底面是等腰直角三角形，∠A1C1B1=90°，A1C1=1，AA1=，D是线段A1B1的中点．
（1）证明：面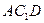⊥平面A1B1BA；
（2）证明：；
（3）求棱柱ABC—A1B1C1被平面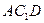分成两部分
的体积比．
粤公网安备 44130202000953号