用秦九韶算法计算多项式
在当
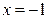时的值，有如下的说法：①要用到6次乘法和6次加法；②要用到6次加法和15次乘法；③
； ④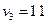
，其中正确的是（ ）
| A．①③ | B．①④ | C．②④ | D．①③④ |
等于（）
则复数
为实数的充要条件是（）
的外接圆的圆心为
,
,
,
,则
等于（）
项和为
等于 （）
, 
则
的最大值，最小值分别是（）
推荐套卷
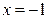用秦九韶算法计算多项式在当时的值，有如下的说法：①要用到6次乘法和6次加法；②要用到6次加法和15次乘法；③； ④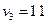，其中正确的是（ ）
| A．①③ | B．①④ | C．②④ | D．①③④ |
粤公网安备 44130202000953号