(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为 ,盈利额为
,盈利额为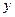 元。
元。
(Ⅰ)求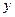 与
与 之间的函数关系;
之间的函数关系;
(Ⅱ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
(参考数据: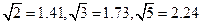 .)
.)
推荐套卷
(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为 ,盈利额为
,盈利额为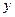 元。
元。
(Ⅰ)求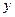 与
与 之间的函数关系;
之间的函数关系;
(Ⅱ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
(参考数据: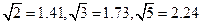 .)
.)