定义：若数列
对任意的正整数n，都有
（d为常数），则称为“绝对和数列”，d叫做“绝对公和”，已知“绝对和数列”
，“绝对公和”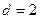
，则其前2010项和
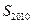的最小值为 （ ）
| A．—2011 | B．—2006 | C．—2010 | D．—2009 |
相关试题
，其中log2f(x)=2x，x
R，则g(x)（）
N
N
推荐套卷
定义：若数列对任意的正整数n，都有（d为常数），则称为“绝对和数列”，d叫做“绝对公和”，已知“绝对和数列”，“绝对公和”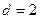，则其前2010项和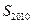的最小值为 （ ）
| A．—2011 | B．—2006 | C．—2010 | D．—2009 |
粤公网安备 44130202000953号