已知抛物线C: y=-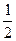
x2+6, 点P（2, 4）、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
相关试题
为第三象限角，试判断
的符号.
的终边在y轴上，求sin
是第三象限角，问
是哪个象限的角？
.
，求a、b的值；相关知识点
推荐套卷
已知抛物线C: y=-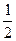x2+6, 点P（2, 4）、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
粤公网安备 44130202000953号