有以下命题：①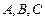
是表面积为
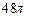的球面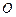
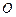(为球心)上的三点，若
，则三棱锥
的体积为
；②二项式
的展开式的各项的系数和为
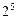；③已知函数
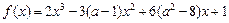在
处取得极值，则实数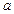
的值是
或
；④已知点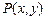
是抛物线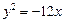
的准线与双曲线
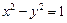的两条渐近线所围成的三角形区域(含边界)内的任意一点，则
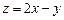的最大值为9。其中正确命题的序号有__________
ABC中．
．则A的取值范围是
}的前n项和
满足：
，且
=1．那么
=
，且
，则
的值为__________
前9项的和等于前4项的和.若
，则
.相关知识点
推荐套卷
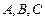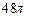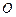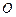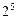有以下命题：①是表面积为的球面(为球心)上的三点，若，则三棱锥的体积为；②二项式的展开式的各项的系数和为；③已知函数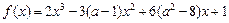在处取得极值，则实数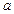的值是或；④已知点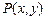是抛物线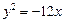的准线与双曲线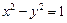的两条渐近线所围成的三角形区域(含边界)内的任意一点，则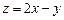的最大值为9。其中正确命题的序号有__________
粤公网安备 44130202000953号