某学生对函数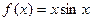
进行研究后，得出如
下结论：
①函数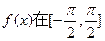
上单调递增；
②存在常数M>0，使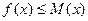
对一切实数x均成立；
③函数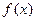
在（0，
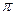）上无最小值，但一定有最大值；
④点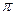（，0）是函数
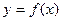图象的一个对称中心
其中正确命题的序号是 。
均为正实数，且
，则
的最小值为．
，
，
与
的夹角为
，
，则
的夹角为．
⊥平面
，直线m
平面
，有下面四个命题：
中，若
，则该数列的前15项的和为．
，则
的值为．相关知识点
推荐套卷
某学生对函数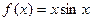进行研究后，得出如
下结论：
①函数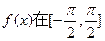上单调递增；
②存在常数M>0，使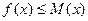对一切实数x均成立；
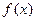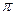③函数在（0，）上无最小值，但一定有最大值；
④点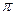（，0）是函数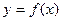图象的一个对称中心
其中正确命题的序号是 。
粤公网安备 44130202000953号