为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别
|
频数
|
频率
|
145.5~149.5
|
1
|
0.02
|
149.5~153.5
|
4
|
0.08
|
153.5~157.5
|
20
|
0.40
|
157.5~161.5
|
15
|
0.30
|
161.5~165.5
|
8
|
0.16
|
165.5~169.5
|
m
|
n
|
合 计
|
M
|
N
|
(1)求出表中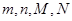 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?