已知定义在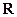 上的函数
上的函数 满足:
满足: ,且对于任意实数
,且对于任意实数 ,总有
,总有 成立.
成立.
(1)求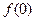 的值,并证明函数
的值,并证明函数 为偶函数;
为偶函数;
(2)若数列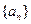 满足
满足 ,求证:数列
,求证:数列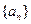 为等比数列;
为等比数列;
(3)若对于任意非零实数 ,总有
,总有 .设有理数
.设有理数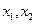 满足
满足 ,判断
,判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
推荐套卷
已知定义在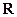 上的函数
上的函数 满足:
满足: ,且对于任意实数
,且对于任意实数 ,总有
,总有 成立.
成立.
(1)求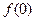 的值,并证明函数
的值,并证明函数 为偶函数;
为偶函数;
(2)若数列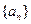 满足
满足 ,求证:数列
,求证:数列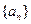 为等比数列;
为等比数列;
(3)若对于任意非零实数 ,总有
,总有 .设有理数
.设有理数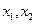 满足
满足 ,判断
,判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.