如图,已知点 ,直线 , 为平面上的动点,过 作直线 的垂线,垂足为点 ,且 .
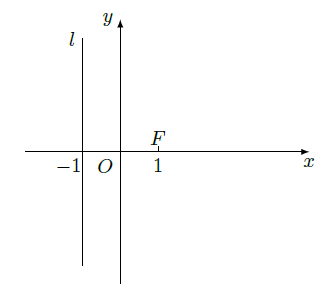
(Ⅰ)求动点
的轨迹
的方程;
(Ⅱ)过点
的直线交轨迹
于
两点,交直线
于点
,已知
,
,求
的值;
推荐套卷
如图,已知点 ,直线 , 为平面上的动点,过 作直线 的垂线,垂足为点 ,且 .
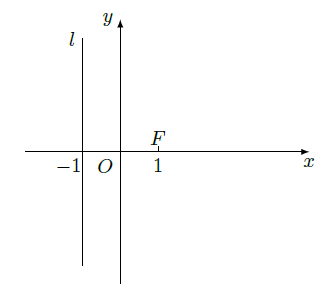
(Ⅰ)求动点
的轨迹
的方程;
(Ⅱ)过点
的直线交轨迹
于
两点,交直线
于点
,已知
,
,求
的值;