(本题满分12分)（学选修4-4的选做题1，没学的选做题2）
题1：已知点M是椭圆C:+ ＝1上的任意一点,直线l:x+2y-10＝0.
(1)设x＝3cosφ,φ为参数,求椭圆C的参数方程；
(2)求点M到直线l距离的最大值与最小值.
题2：函数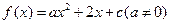
的一个零点是１，另一个零点在（－1,0）内，（1）求
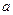的取值范围；
（2）求出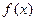
的最大值或最小值，并用
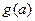表示．
，
，
，都有
；
都有
．
为
上的单调增函数；
；
，
）
；（2）求
的取值范围
能表示成一个奇函数
和一个偶函数
的和，求
的解析式；
上是增函数与命题Q：.函数
相关知识点
推荐套卷
(本题满分12分)（学选修4-4的选做题1，没学的选做题2）
题1：已知点M是椭圆C:+ ＝1上的任意一点,直线l:x+2y-10＝0.
(1)设x＝3cosφ,φ为参数,求椭圆C的参数方程；
(2)求点M到直线l距离的最大值与最小值.
题2：函数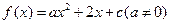的一个零点是１，另一个零点在（－1,0）内，（1）求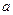的取值范围；
（2）求出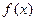的最大值或最小值，并用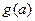表示．
粤公网安备 44130202000953号