在古希腊毕达哥拉斯学派把1，3，6，10，15，21，28，…这些数叫做三角形数，因为这些数对应的点可以排成一个正三角形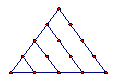
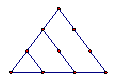
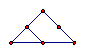
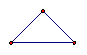
1 3 6 10 15
则第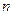
个三角形数为
| A． |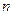
B． |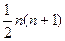
C． |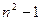
D． |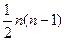
,则“
”是“
”的( )
，则
( )
，则
( )
，若
，则实数
的取值范围为( )
，
，若
与
的夹角为
，则
的最大值为( )
推荐套卷
在古希腊毕达哥拉斯学派把1，3，6，10，15，21，28，…这些数叫做三角形数，因为这些数对应的点可以排成一个正三角形
1 3 6 10 15
则第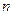个三角形数为
| A． |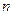
B． |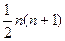
C． |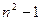
D． |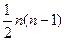
粤公网安备 44130202000953号