(本小题满分12分)
要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为24500cm2四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告牌的高与宽的尺寸(单位:cm),能使矩形广告牌面积最小?并求出最小面积。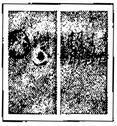
推荐套卷
(本小题满分12分)
要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为24500cm2四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告牌的高与宽的尺寸(单位:cm),能使矩形广告牌面积最小?并求出最小面积。