(本小题满分12分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从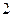 种服装商品,
种服装商品, 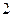 种家电商品,
种家电商品, 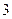 种日用商品中,选出
种日用商品中,选出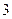 种商品进行促销活动.
种商品进行促销活动.
(Ⅰ)试求选出的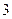 种商品中至多有一种是家电商品的概率;
种商品中至多有一种是家电商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高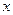 元,同时,若顾客购买该商品,则允许有
元,同时,若顾客购买该商品,则允许有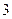 次抽奖的机会,若中奖,则每次中奖都获得数额为
次抽奖的机会,若中奖,则每次中奖都获得数额为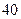 元的奖券.假设顾客每次抽奖时获奖的概率都是
元的奖券.假设顾客每次抽奖时获奖的概率都是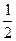 ,若使促销方案对商场有利,则
,若使促销方案对商场有利,则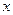 最少为多少元?
最少为多少元?
推荐套卷
(本小题满分12分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从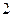 种服装商品,
种服装商品, 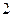 种家电商品,
种家电商品, 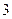 种日用商品中,选出
种日用商品中,选出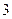 种商品进行促销活动.
种商品进行促销活动.
(Ⅰ)试求选出的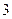 种商品中至多有一种是家电商品的概率;
种商品中至多有一种是家电商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高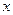 元,同时,若顾客购买该商品,则允许有
元,同时,若顾客购买该商品,则允许有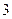 次抽奖的机会,若中奖,则每次中奖都获得数额为
次抽奖的机会,若中奖,则每次中奖都获得数额为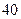 元的奖券.假设顾客每次抽奖时获奖的概率都是
元的奖券.假设顾客每次抽奖时获奖的概率都是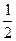 ,若使促销方案对商场有利,则
,若使促销方案对商场有利,则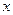 最少为多少元?
最少为多少元?