(本小题满分12分)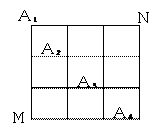
如图，在某城市中，Ｍ，Ｎ两地之间有整齐的方格形道路网，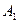
、
、
、
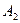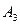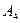是道路网中位于一条对角线上的４个交汇处，今甲由道路网Ｍ处出发随机地选择一条沿街的最短路径到达Ｎ处.
（Ⅰ）求甲由M处到达N处的不同走法种数；
（Ⅱ）求甲经过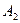的概率.
，且直线
与
都相交，求证：直线
共面。
为空间四边形
的边
上的点，且
．求证：
. 
，求
的最小值。推荐套卷
(本小题满分12分)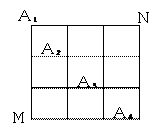
如图，在某城市中，Ｍ，Ｎ两地之间有整齐的方格形道路网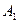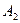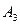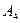，、、、是道路网中位于一条对角线上的４个交汇处，今甲由道路网Ｍ处出发随机地选择一条沿街的最短路径到达Ｎ处.
（Ⅰ）求甲由M处到达N处的不同走法种数；
（Ⅱ）求甲经过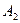的概率.
粤公网安备 44130202000953号