矩阵与变换
在平面直角坐标系xOy中，A(0,0),B(-3,),C(-2,1),设k≠0，k∈R，M=
,N=
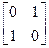,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍，求实数k的值
中，
，
分别是
的中点，
，求异面直线
所成的角.
满足
，且
。
上，
的图象恒在
的图象上方，试确定实数
的范围。
，
的奇偶性；
上是减函数。
求函数
的最大值和最小值。推荐套卷
矩阵与变换
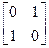在平面直角坐标系xOy中，A(0,0),B(-3,),C(-2,1),设k≠0，k∈R，M=,N=,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍，求实数k的值
粤公网安备 44130202000953号